Hackergame 2020 (第七届中科大信安赛) Writeup 0x01
Hackergame 2020 write up 0x01
书接上文,接下来也是一些很有趣的题目,但是可能需要一些基础。
希望其中的技术性知识会引起你的好奇心而不是劝退(。・ω・。)
(虽然数理模拟器真的不是什么好回忆)
超简陋的 OpenGL 小程序
年轻人的第一个 OpenGL 小程序。
(嗯,有什么被挡住了?)
看起来是一个可执行程序欸!
打开之后看到如下结果:
嗯,, , 的确有东西被挡住了呢!但怎么能See through walls呢?
其实可以打开basic_lighting.vs文件看看里面有什么东西…
哦,一个main()函数
内容是…
FragPos = vec3(model * vec4(aPos, 1.0));
Normal = aNormal;
gl_Position = projection * view * vec4(FragPos, 1.0);其实利用这个文件我们是可以修改视角的!
FragPos = vec3(model * vec4(aPos, 1));
Normal = aNormal;
vec4 a = vec4(FragPos, 0.05);
a.y -= 0.65;
a.z -= 1.55;
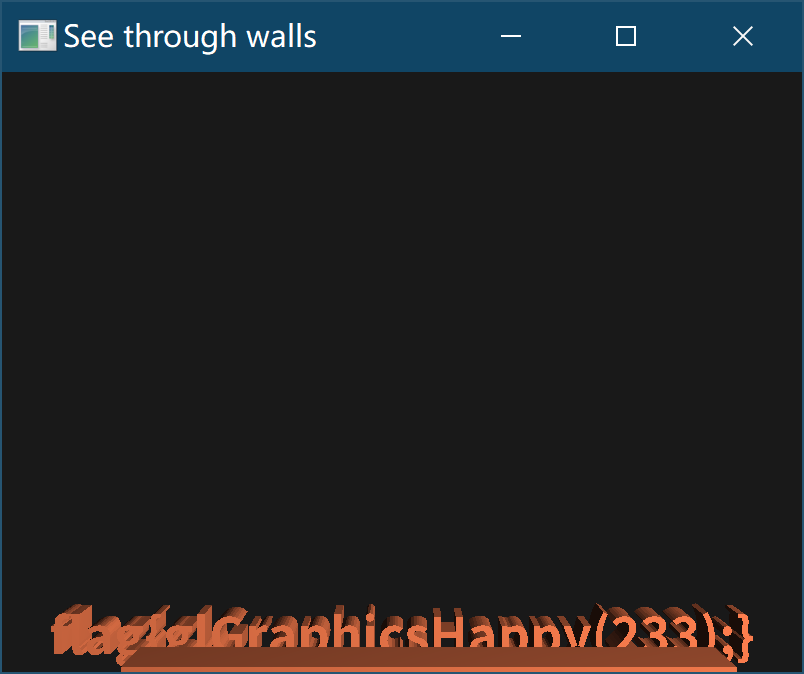
gl_Position = projection * view * a;如上所示更改了顶点着色器之后:
就可以看到最终的flag了
flag{glGraphicsHappy(233);}
PS: 这道题目其他选手的做法真是让我大呼我还是太年轻了… 官方 深度烧烤
超基础的数理模拟器
这一切的一切,还要从 Hackergame 2020 群说起。
不知是从什么时候,也许是上一次 Hackergame,或是更早,Hackergame 2020 群里的科气逐渐变得浓厚起来。等到真正引起管理员注意时,上千人的群已经完全沦为了菜市场。群里充斥着各式各样的卖菜声,比如 “tql”,“wtcl”,“sdl, wsl”,“orz”,“ddw”,各式各样的卖弱表情包交相辉映。再加上群内复读机和正常人的比例严重失调,致使事态进一步恶化,场面一度无法控制。
在管理员和其余正常群友的齐心协力之下,此类现象在群内的出现频率最终显著下降。但不幸的是,由于其他群的群主警惕不足,或是管理不慎 (某大群群主甚至大肆宣扬 “科气 is fake”,听说最近连自己也未能幸免科了起来,也不知还能不能继续当选下一任群主),每天仍然有许多群友在花式卖弱,而一些心理素质较差的群友也因此永远地退出了群聊。
各大水群的诸多龙王联合起来,研究多月之后,终于找到了此次事件的罪魁祸首:那位身处大洋彼岸,就读于 UCB,不可提及姓名的老学长。而他的根本目的,就是试图利用同学们充满科气的卖弱行为,在如今废理兴工已经式微的科大,再次掀起反思数理基础教育的思想浪潮。故而本次事件被命名为:FLXG-20。
为了应对那位学长的所作所为,我们在 Hackergame 2020 的网站上部署了一项超基础的数理模拟器。作为一名数理基础扎实的同学,你一定能够轻松通过模拟器的测试吧。
说实话这是让我最无奈的一道题,因为我就是手动搞了两小时的那个.
有点想锤出题人呢 (跑
在多般调试和实验失败,无法成功使得Mathematica与Python交互的情况下只得跑Mathematica然后复制粘贴做题了…QAQ
s = InputString[];
intRange = StringSplit[s][[1]];
intLeft =
ToExpression[StringSplit[intRange, {"_", "^"}][[2]], TeXForm];
intRight =
ToExpression[StringSplit[intRange, {"_", "^"}][[3]], TeXForm];
expr = StringReplace[
StringTake[
StringJoin@Take[StringSplit[s], {2, -1}], {1, -7}], {"e^" -> "E^",
"{" -> "{(", "}" -> ")}", "\\ln\\left(x\\right)" -> "{\\ln(x)}",
"\\left(" -> "(", "\\right)" -> ")"}];
expr = ToExpression[expr, TeXForm];
value = NIntegrate[expr, {x, intLeft, intRight}, PrecisionGoal -> 10,
WorkingPrecision -> 20]
NumberForm[value, {10, 6}]于是…
内心:啊手动搞了两百道题了纪念一下
内心:啊啊啊只剩六十道了但是我手好酸肩膀好痛
内心:啊啊啊只剩最后十道了!!! 我要在结束时候截图留念!!
BUT 通关之后并没有任何美观的前端只有一个简洁又气人的flag而已
```(╯‵□′)╯︵┻━┻ (╯‵□′)╯︵┻━┻ (╯‵□′)╯︵┻━┻ (╯‵□′)╯︵┻━┻`
但毕竟…过了(微笑拔刀
flag{S0lid_M4th_Phy_Foundation_31ab055b46}
永不溢出的计算器
某同学写了一个简单的计算器程序,支持加、减、乘、除、乘方、开方运算。
但是,计算器计算大数的时候会溢出,这位同学不想看到计算器溢出,于是他想了一个绝妙的方法。而更绝妙的是,这里的空间足够写下这个方法:
让计算器的所有计算都是在 mod n 意义下进行
出于某种众所周知的原因,他还用这个计算器算了一下 flag 字符串对应的整数的 65537 次方
嗯, 好呗, 又是模n又是65537, 所以总所周知的原因就是你给我搞了个RSA是吧(╯‵□′)╯︵┻━┻
其实这道题的理论基础是可以被找到的: 参考资料
以下将以RSA中的变量称呼来进行, 目前情况下, 我们知道了 目标是找到 来解密 进而得到flag
幸运的是, 我们有一个可以直接在模 下计算的计算器, 首先, 我们需要知道 是多少:
而解决这道题的另一个很重要很基础但是不好想的数学公式是:
当我们知道 并且 的时候, 很容易就能知道:
求出 之后RSA便不攻自破了, 只需要计算一下 再用扩展欧几里得算一下 关于 的乘法逆元, 再计算一下
那么 从哪里来呢…?反正我用的是
(其实我也没想明白, 学长说是有概率拿到一个合适的)
ranwen, [07.11.20 22:26]
所有 n 里头 不含 pq 因子的数
ranwen, [07.11.20 22:26]
有 1/4 都是可开的
mcfx, [07.11.20 22:27]
所以只是运气好最后用python的库转换一下大整数
from Crypto.Util.number import long_to_bytes
print(long_to_bytes(flag))于是可以得到flag
flag{SQRT_0racle_w1ll_l3ak_f4ct0r_0f_N_2db518ada9}
附: 用到的算法的 示例代码
PS: python算大整数真的是太方便了, 不愧是世界上最好用的计算器(逃
PSS: 可能是第一次吧, 算出来并验证了它们是素数的时候我兴奋了好一会ヾ(≧▽≦*)o
超精巧的数字论证器
数字论证是一种常见的定理证明方法。简单来说,就是对于给定的自然数,找出一个等值的表达式,如果该表达式去除所有符号部分后为字符串「114514」,则完成论证。表达式仅允许整数运算,可以使用括号、常见的代数运算符 ±*/% 和位运算符 ~^&|。表达式具体运算规则与 Python 2 语言类似。
一些数字论证的例子:
0 = (1/14514) 1 = (1%14514) 2 = (11&4514) 3 = (1+(14&514)) 4 = (1^(145%14)) 5 = -(1145|-14) 6 = (-1145&14) 7 = (11-(4%514)) 8 = (1145&14) 9 = -(-11|4514) 10 = (11&-4514) 11 = (11%4514) 12 = (11-(45|-14)) 13 = (-1+(14%514)) 14 = (1*(14%514)) 15 = (1+(14%514)) 16 = (1+(14|(5%14))) 17 = ((11&-45)+14) 18 = (114&(5+14)) 19 = (1+(14+(5&14)))数字论证并不是一件容易的事情,你可以完成这个任务吗?
给定的自然数保证小于 114514。输入的表达式长度不可以超过 256 字符。
又是知识盲区,去搜什么是数字论证,然后找到了这个东西:恶臭数字论证器
啊,无论如何,既然是需要给数字之间填充运算符,先写个程序把数字分好组吧。
combines = [
['114514'], ['11451', '4'], ['1', '14514'],
['11', '4514'], ['114', '514'], ['1145', '14'],
['1145', '1', '4'], ['1', '1451', '4'], ['1', '1', '4514'],
['11', '4', '514'], ['114', '5', '14'], ['1', '14', '514'],
['11', '45', '14'], ['114', '51', '4'], ['1', '145', '14'],
['11', '451', '4'], ['114', '5', '1', '4'], ['1', '145', '1', '4'],
['1', '1', '451', '4'], ['1', '1', '4', '514'], ['11', '45', '1', '4'],
['11', '4', '51', '4'], ['11', '4', '5', '14'], ['1', '14', '5', '14'],
['1', '1', '45', '14'], ['1', '14', '51', '4'], ['11', '4', '5', '1', '4'],
['1', '14', '5', '1', '4'], ['1', '1', '45', '1', '4'], ['1', '1', '4', '51', '4'],
['1', '1', '4', '5', '14'], ['1', '1', '4', '5', '1', '4']]然后就要往这些数字之间添加运算符了,首先除法/本身没什么必要,还会增加产出为非整数的风险,放弃。对于按位取反的~在加减1的时候是需要特殊使用的,不放在需要插入的列表中。
剩余的运算符为['+', '-', '*', '%', '^', '|', '&']
想了想还是直接写个简单的dfs来添加运算符,然后用eval()进行计算,如果结果为负数就添加个-(xxx)再进行记录,并把每种产出的结果作为key存储到字典中。
下面是dfs的代码
def dfs(str, nums, f):
'''已经拼接好的字符串 str, 剩下的数字 nums, 待写入文件 f'''
if len(nums) == 0:#如果已经没有更多数字了
try:
value = eval(str)#计算表达式
if abs(value) in dictionary or abs(value) > 114514:
#若已经存在或绝对值大于 114514 (其实不可能)
return
if value < 0:# 如果值小于 0 添加符号后记录
str = '-(' + str + ')'
dictionary[-value] = str
f.write(f' "{-value}": "{str}", \n')
else:# 否则直接记录
dictionary[value] = str
f.write(f' "{value}": "{str}", \n')
if len(dictionary) % 500 == 0:
#定量输出进度让我知道程序没有偷懒
print('found {} expr.'.format(len(dictionary)))
return
except:
return
for op in oper:#对每一种运算符
dfs(str + op + nums[0], nums[1:], f)#先不添加 ~- 和 -~
for i in range(1, 20):#添加 ~- 和 -~ 所得值分布在 [nums[0] - 20, nums[0] + 20]
if int(nums[0]) > i: # 保证减了之后是正数
#添加 i 个 ~- (-1)
dfs(str + op + '(' + '~-'*i + nums[0] + ')', nums[1:], f)
#添加 i 个 -~ (+1)
dfs(str + op + '(' + '-~'*i + nums[0] + ')', nums[1:], f)其实这个递归的运算量是巨大的,但是当跑到把114514分成 5 个数字之前,就已经可以发现len(dictionary)的长度达到了48k左右且增长十分缓慢,这时候算出来的大多数都是重复值了,而我们总的需求量也不过115k, 再者,观察输出发现很少有长度可以超过100的于是我们可以利用~-和-~运算符进行数字的稠密化。
keys = sorted(data.keys())
for i in keys: #对于每一个已经算出来的值
for r in range(1, 31): #半径 30
# 若没有 r + i 或者 r - i 就添加对应数量的 ~- 或 -~
if (i + r) not in data_r:
data[i + r] = '-~'*r + '(' + data[i] + ')'
if (i - r) > 0 and (i - r) not in data_r:
data[i - r] = '~-'*r + '(' + data[i] + ')'这样富集后这个final_out.json涵盖的数字个数已经达到了114k+, 基本上过他 32 个不成问题了!!!
然后…
我开始了手动输入…
(你体验过超时的绝望吗…)
于是在不知道多少次的尝试之后,我成功拿到了flag
flag{Tw0_s_c0mplement_representati0n_1s_1mp0rtant_9ab8645e92}
嗯,当天晚上我知道了有个东西叫做pwntools
在linux下运行时,它有个函数是remote
可以连接nc并且直接进行输入和读取输出
嗯,所以我手动一次好几分钟的事情被我写成了1s提交的代码
嗯,我在干什么啊啊啊ヾ(≧へ≦)〃
from pwn import *
import json
token = input('token:')
io = remote('202.38.93.111', '10241')
data = json.loads(open('final_out.json').read())
print(io.recv())
io.send(token + '\n')
for _ in range(32):
input_str = io.recv().decode('utf-8')
print(input_str.replace('\\n', '\n'), end=' ')
num = ''
for chars in input_str.split(':')[1].split(' '):
if chars != '':
num = chars
break
print(data[num][:6]+ '...')
io.send(data[num] + '\n')
print(io.recv().decode('utf-8').replace('\\n', '\n'))超自动的开箱模拟器
想体验开箱的快乐吗?
这是一个开箱模拟器。当你输入「BF 开箱码」之后,程序会模拟 128 轮游戏,每轮你有 64 次开箱机会。
如果你 128 轮中每轮都能够在 64 次机会之内找到目标所在的箱子,那么你将会得到 flag。
这也是我比较喜欢的一道题了 qwq
刚开始拿到这道题,先读了读代码,感觉这简直就是不可能的事情。
然后看了看基础的逻辑,就是通过BrainFuck 代码来输出 1, 2, 3 进行开箱的流程控制。
其中1是后退一格,2是前进一格,3是输出当前格
先试试手,写了一个轮流开箱的 BFCode:++>+++[.<.>]
果然,成功概率约等于0
再读代码,看到了每一轮系统会把开出来的东西扔进 BF 控制的数据的input中
but 没有任何想法,但是因为这个输入,想写一个每次开对应输入的 BFCode
而这也就是真正的解法,这个问题的名字叫做百囚徒问题其实按照对应的策略去开箱,让开箱的内容变成环的问题,这个事情的可行概率就变得很大,所以我们现在要实现这个策略
思索…
- 读入一个数字到
data_n - 循环输出
data_n个2 - 输出
3开箱 LOOP
也就是用使得 data = [2, 3, n]
即:+++>++>[,[<.>-]<<3>>]
也很快就发现了问题,开箱指针的位置只加不减,我需要让它回到原来的位置再进行下一轮移动
思索…
- 读入一个数字到
data_n - 循环输出
data_n个2 - 输出
3开箱 - 循环输出
data_n个1 LOOP
但是很快在写 BF 的时候问题又来了,我在输出2的过程中已经把data_n清零了,如果再循环没有东西可以用来当作循环次数的限制了,于是:
思索…
- 读入一个数字到
data_x - 循环
data_x次- 输出
2 data_y加一
- 输出
- 输出
3开箱 - 循环输出
data_y个1 LOOP
也就是用使得 data = [x, 1, 2, 3, y]
即:,>+>++>+++<<<[[>>.>>+<<<<-]>>>.>[<<<.>>>-]<<<<,]
但是又发现了问题:
- Guess 27/64: 45->73
- Guess 28/64: 73->22
- Guess 29/64: 22->128
- Guess 30/64: 127->69
- Guess 31/64: 69->83
- Guess 32/64: 83->86到达128的时候会直接跳转到127而不是预期的128, 再次查看源代码,发现:
elif out == 2: # move right
if box_key < self.nboxes - 1:
box_key += 1而self.nboxes是128, 也就是说我们需要开箱的范围是[0, 127]而序号的范围是[1, 128]为此我们需要做的映射是开的箱号是拿到的序号减一的值,于是就加了个输出1的上去,觉得万事俱备只欠东风,兴致冲冲地实验了几百次,无一例外的失败了…(゚Д゚*)ノ
我改的 BFCode 如下:>,>+>++>+++<<<[[>>.>>+<<<<-]>.>>.>[<<<.>>>-]<<<<,]
你能看出来问题出在了哪里吗?
这是一段输出:
- Guess 32/64: 72->62
- Guess 33/64: 61->49
- Guess 34/64: 48->128
- Guess 35/64: 126->91
- Guess 36/64: 90->124
- Guess 37/64: 123->85它成功把除了128之外的n映射到了n-1却把128映射到了126
为什么?
代码的逻辑是先走出去n之后回退1
因为我在到127之后想要前进一步再后退,于是继续输出了一个2, 这个2被判定为无效输出,位置还在127, 但我又跟着输出1进行后退,于是到达了126
解决这个问题的办法在于在读取数据之后直接给输入减一,这样开箱指针的目标位置就直接变成了n-1, 便可以解决这个问题
思索…
- 读入一个数字到
data_x - 读入的数字减去
1 - 循环
data_x次- 输出
2 data_y加一
- 输出
- 输出
3开箱 - 循环输出
data_y个1 LOOP
于是,我的通关 BFCode 诞生了:,>+>++>+++<<<[-[>>.>>+<<<<-]>>>.>[<<<.>>>-]<<<<,]
拿到flag:
flag{y0u_R_def1n1tely_th3_MA5T3R_0f_unb0x1ng_e9e7ba011d}
这之后便到了喜闻乐见的比长短时间:
NanoApe, [04.11.20 23:42]
过了
GZ Time, [04.11.20 23:42]
来我看看长度如何
NanoApe, [04.11.20 23:44]
Len=118
GZ Time, [04.11.20 23:45]
Len=49
GZ Time, [04.11.20 23:45]
Nano好长(
NanoApe, [04.11.20 23:46]
思考 我以为写得挺短了
NanoApe, [04.11.20 23:47]
结果还是太长了Q: 如何压缩这个 BFCode?
A: 目前我们的 BFCode 用了 5 个数据位,这之间的移动的步骤就很浪费长度可以将1, 2, 3放在一个数据位置,然后进行操作。
于是压缩后的 BFCode 长这样:,>++<[-[>.>+<<-]>+.-->[<.>-]<+<,]
然而目前我知道的最短记录保持者是mcfx, 他知道我们在比长短之后,把自己的47硬生生压到了27, 据说只用了两个数据位。
mcfx, [05.11.20 20:41]
我现在27了Have A TRY?
>>> 0x01 END